[Paper Review] Spatial transformer networks
Spatial transformer networks
Jaderberg, Max, Karen Simonyan, and Andrew Zisserman. “Spatial transformer networks.” Advances in neural information processing systems 28 (2015).
Abstract
CNN은 매우 강력하지만, 계산 및 파라미터 효율적인 방식으로 입력 데이터에 공간적으로 불변하는 능력이 부족하여 여전히 제한적임
공간적 변형에 취약한 CNN
invariance는 불변성이라는 뜻으로 함수의 입력이 바뀌어도 출력은 그대로 유지되어 바뀌지 않는다는 뜻이고,
공간적으로 변형된 입력 데이터에 대해서도 동일한 결과값을 내는 것을 의미
참고 자료 : https://seoilgun.medium.com/cnn%EC%9D%98-stationarity%EC%99%80-locality-610166700979
논문에서는 네트워크 내에서 데이터의 공간적 조정을 명시적으로 허용하는 학습 가능한 Spatial Transformer 모듈을 제안
Spatial Transformer 모듈은 미분이 가능하고, 기존의 CNN 구조에 삽입이 가능
최적화 과정에서 추가적인 학습 지도나 수정없이 feature map 자체에 맞추어 feature map을 공간적으로 변형시키는 기능을 제공
spatial transformers의 사용이 공간적 변형(translation, scale, rotation, more generic warping)에 대한 invariance을 학습할 수 있게 하는 것을 실험으로 확인했고, SOTA 성능 달성
Introduction
최근, CNN(fast, scalable, end-to-end)의 등장으로 컴퓨터 비전에 큰 발전이 있었음
classification, localisation, semantic segmentation, action recognition 등 다양한 분야에서 CNN 기반 모델이 SOTA를 달성하는 것을 볼 수 있음
이미지를 추론할 때 중요한 능력은 texture와 shape으로부터 object pose와 part deformation을 구분하는 것임
object pose : 객체가 속해있는 부분이 어디인지 판별 (객체의 모양)
CNN에서 local max-pooling layer의 도입이 네트워크가 features의 위치에 다소 공간적으로 불변하도록 하여 추론 능력에 도움이 됨
하지만, max-pooling은 작은 공간(2x2 pixels)에 대해서 적용하기 때문에 공간 불변성은 max-pooling과 convolution layer를 깊게 쌓은 구조에서만 실현됨
이러한 사전 정의된 pooling mechanism이 CNN의 한계점 (고정적인 연산)
본 논문에서는 neural network에 공간적 변형 능력을 제공하기 위한 Spatial Transformer module 소개
-
Spatial Transformer
추가적인 지도학습 없이 task를 위해 학습하는 과정에서 학습된 적절한 행동에 의해 입력 데이터에 따라 컨디션 됨
receptive field가 고정적이고 지역적인 pooling layer와 달리, image or feature map을 공간적으로 변형할 수 있는 동적인 메커니즘
입력 데이터에 따라 다르게 변형됨
변형이 전체 feature map에 대해 수행되고 (non-locally), scaling, cropping, rotations, non-rigid 변형을 포함할 수 있음
모델에 삽입하고 표준적인 back-propagation으로 학습이 가능 (end-to-end 학습)
-
Spatial Transformer module의 효과
-
task를 수행하기 위해 가장 중요한 영역을 선택할 수 있게 함 (attention)
-
다음 layer에서 더 쉽게 인식할 수 있는 형태로 변형하여 전달
-
-
Spatial transformers은 다양한 task에 적용할 수 있음
-
image classification
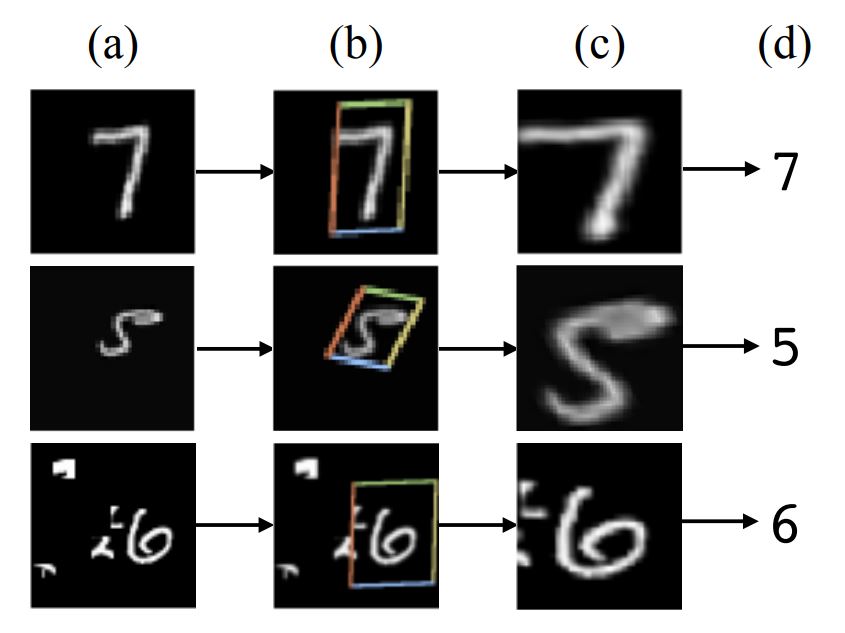
숫자 이미지 분류(MNIST)에서 숫자의 위치와 사이즈는 데이터 샘플마다 매우 다양함
Spatial transformers는 적절한 영역을 크롭하고 스케일을 조정하고, 이는 classification task를 더 쉽게 만들어주며 좋은 성능으로 이어짐
-
co-localisation
동일한 클래스의 다른 instances가 포함되어 있는 이미지들이 주어졌을 때, spatial transformer가 각 이미지에서 instance들을 localisation 하는데 사용될 수 있음
-
spatial attention
attention mechanism을 필요로 하는 task에 사용될 수 있고, 이는 강화학습 없이 backpropagation 만으로 더 유연하게 학습될 수 있음
-
Spatial Trnasformers
single forward pass 동안 feature map에 대해 공간적 변형을 수행하는 미분가능한 모듈
특정 입력에 따라 다르게 변형이 수행되고, input feature을 변형시킨 output feature map을 생성
입력의 채널이 여러개라면, 채널별로 동일한 변환을 적용시킴
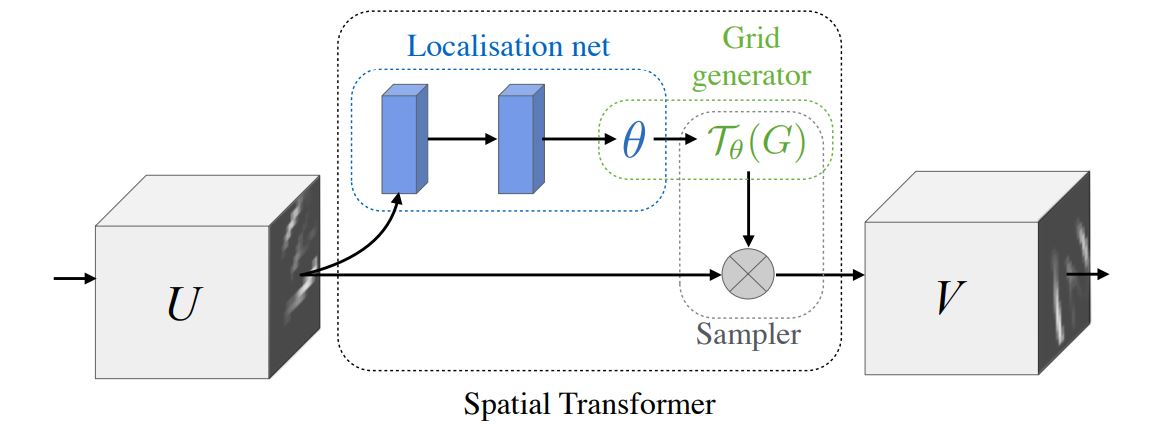
localisation network
feature map을 입력으로 받아서 수많은 hidden layers를 거쳐 feature map에 적용시킬 공간 변형 파라미터를 출력
입력에 따라 변형 파라미터가 다르게 생성됨
공간 변환 파라미터를 예측(regress) 하는 일반적인 CNN
공간 변환은 데이터 셋으로부터 명시적으로 학습되지 않고, 신경망이 전체 정확도를 향상 시키도록 공간 변환을 자동으로 학습
참고 자료 : https://tutorials.pytorch.kr/intermediate/spatial_transformer_tutorial.html
grid generator
변형 파라미터를 이용하여 sampling grid를 만듦
sampling grid : 점들의 집합으로, 변형된 output을 만들기 위해 input map에서 샘플링된 points
출력 이미지로부터 각 픽셀에 대응하는 입력 이미지 내 좌표 그리드를 생성
참고 자료 : https://tutorials.pytorch.kr/intermediate/spatial_transformer_tutorial.html
sampler
grid points에서 input으로부터 샘플링된 output map 생성
공간 변환 파라미터를 입력 이미지에 적용
참고 자료 : https://tutorials.pytorch.kr/intermediate/spatial_transformer_tutorial.html
Localisation Network
\[\theta = f_{loc}(U)\]-
Input : feature map $U \in R^{H \times W \times C}$
-
output : trasformation $\tau_{\theta}$의 파라미터인 $\theta$
$\theta$의 사이즈는 변형 타입에 따라 다양함
affine transformation의 경우 6-dimensional
$f_{loc}$은 어떤 형태의 입력도 받을 수 있지만, 변형 파라미터인 $\theta$를 생성하기 위한 최종적인 regression layer가 꼭 포함되어 있어야 함
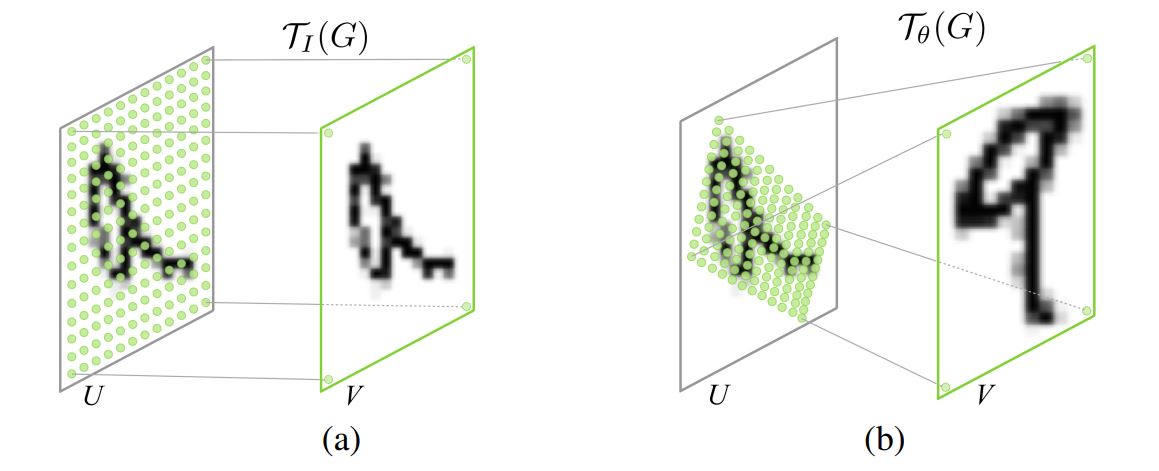
Parameterised Sampling Grid
input feature map warping을 수행하기 위해, input feature map에서의 특정 위치에 중심을 둔 샘플링 커널을 적용하여 output pixel을 계산해야 함
이미지 뿐만 아니라 feature map의 element도 pixel이라고 부름
일반적으로, output pixels은 일반 좌표 ${G = \lbrace G_i \rbrace}$로 정의되고, output feature map $V \in R^{H’ \times W’ \times C}$가 생성됨
pixel $G_i = (x_i^t, y_i^t)$
입력과 출력에서 채널은 동일하게 유지됨
-
2D affine transformation $A_{\theta}$ 예시
$(x_i^t, y_i^t)$ : target coordinates
$(x_i^s, y_i^s)$ : source coordinates (sample points)
Differentiable Image Sampling
input feature map의 공간 변형을 수행하여 output feature map V 생성
-
input : sampling points 집합 $\tau_{\theta}(G)$, input feature map U
-
output : sampled output feature map V

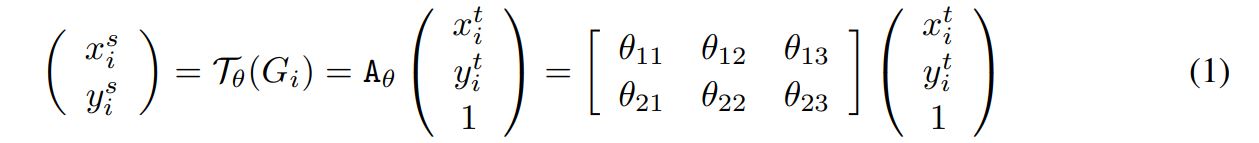
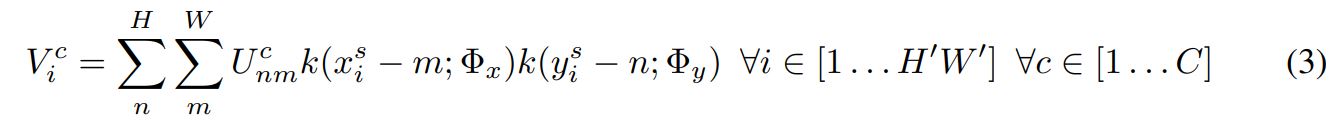
Leave a comment